Sin 2 x = tan x (1 cos 2 x) \sin 2x=\tan x (1\cos 2x) sin 2 x = tan x (1 cos 2 x)Tan2x Formulas Tan2x Formula = 2 tan x 1 − t a n 2 x We know that tan (x) = sin (x)/cos (x) Then, tan2x formula = sin (2x)/cos (2x) Tan 2x can also be written in terms of sin x and cos x, Tan2x Formula in terms of cos x = 2 s i n ( x) c o s ( x) c o s 2 x − s i n 2 x You can check some important questions on trigonometry and trigonometry all formula from below 1 Find cos X and tan X if sin X = 2/3 2 In a given triangle LMN, with a right angle at M, LN MN = 30 cm and LM = 8 cm Calculate the values of sin L, cos L, and tan L 3

Sin2x Cos2x 1 Proof
Sin 2x tan 2x formula
Sin 2x tan 2x formula-The equation we want to solve is \sin(2x)\tan(x) You deduced correctly that we now have to solve 2\sin(x)\cos(x)\frac{\sin(x)}{\cos(x)}=0 which we can rewrite to 2Solve sin(2x) tan(x) = 0 Solving a Trigonometric Equation To solve a trigonometric equation, we first need to simplify it by applying any relevant trigonometric identities
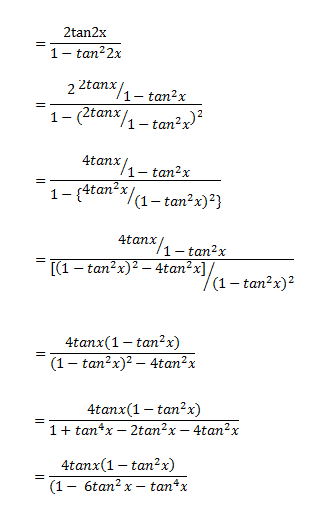



Trigonometry Functions Class Xi Exercise 3 3 Breath Math
Plot of the six trigonometric functions, the unit circle, and a line for the angle θ = 07 radiansThe points labelled 1, Sec(θ), Csc(θ) represent the length of the line segment from the origin to that point Sin(θ), Tan(θ), and 1 are the heights to the line starting from the xaxis, while Cos(θ), 1, and Cot(θ) are lengths along the xaxis starting from the origin #tan x=sinx/cos x, sin 2x = 2 sin x cos x and cos 2x = cos^2xsin^2x#, for the right hand side expression Explanation #2 tan x/(1tan^2x)=(2sin x/cos x)/(1(sin^2x/cos^2x)# Find sin 2x, cos 2x, and tan 2x from the given information tan x = −1/2 , cos x > 0 In trigonometry, the tangent halfangle formulas relate the tangent of one half of an angle to trigonometric functions of the entire angle They are as follows
Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin andFree trigonometric identities list trigonometric identities by request stepbystepSolve for x 2sin(2x)=tan(2x) Rewrite in terms of sines and cosines Substitute Take the inverse sine of both sides of the equation to extract from inside the sine The exact Divide each term in by Cancel the common factor of Tap for more steps Cancel the common factor Divide by Divide by The sine function is positive in the
cos(ax)cos(bx) = 1 2cos((a − b)x) 1 2cos((a b)x) These formulas may be derived from the sumofangle formulas for sine and cosine Example 726 Evaluating ∫ sin(ax)cos(bx)dx Evaluate ∫sin(5x)cos(3x)dx Solution Apply the identity sin(5x)cos(3x) = 1 2sin(2x) 1 2sin(8x)You can put this solution on YOUR website!Equation systems Step by Step;



Www Alamo Edu Contentassets 35e1aad11a064ee2ae161ba2ae3b2559 Analytic Math2412 Double Angle Power Reducing Half Angle Identities Pdf




The Value Of Lim X Pi 2 Tan 2x Sqrt 2sin 2x 3sinx 4 Sqrt Sin 2 X 6sinx 2 Is Equal To
\(\cos 2X = \frac{1\tan ^{2}X}{1\tan ^{2}X} Since, \tan X = \frac{\sin X}{\cos X} \) Hence, \(\cos 2X = \frac{1\tan ^{2}X}{1\tan ^{2}X} \) Solved Examples Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula \(tan(ab) =\frac{ tan a tan b }{1 tan a tanb}\) So, for this let a = b , it becomes \(tan(aa) =\frac{ tan a tan a }{1 tan a tana}\) \(Tan 2a =\frac{2tan a}{1tan^{2}a} \) Practice Example for tan 2 theta QuestionSin(2x) = 2tan(x) /(1 tan 2 (x)) Sin 2x Formula in Terms of Cos Sin 2x formula can be written in the terms of Cos or cosine function only For this formula, we use the basic trigonometric identity of the relation between sin and cos and convert the sinx in the formula of sin2x in terms of cosx The formula for sin2x in terms of cos is Sin 2x = 2 sinx cosx




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic



1
In Trigonometry Formulas, we will learn Basic Formulas sin, cos tan at 0, 30, 45, 60 degrees Pythagorean Identities Sign of sin, cos, tan in different quandrants Radians Negative angles (EvenOdd Identities) Value of sin, cos, tan repeats after 2π Shifting angle by π/2, π, 3π/2 (CoFunction Identities or Periodicity Identities) When trying to prove trig identities, it is often helpful to convert TAN functions into SIN/COS functions Proof Step 1 Start with the original equation to prove tan 2 x sin 2 x = (tan 2 x)(sin 2 x) Proof Step 2 Replace tan with sin/cos (sin 2 x/cos 2 x) sin 2 x = (sin 2 x/cos 2 x)(sin 2 x) Proof Step 3 Obtain a common denominator on left, simplify right (sin 2 x sin 2 x cos 2 x x=npi or x=npipi/4 where n is an integer As sinxtan^2x=sinx sinxtan^2xsinx=0 or sinx(tan^2x1)=0 ie either sinx=0=sin0 ie x=npi or tan^2x=1=tan^2(pi/4) ie tanx=tan(pi/4)or x=npipi/4 where n is an integer




Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Day 3 Hw 1 To 2 Find Sin2x Cos2x And Tan2x Given One Trig Value And The Quadrant Youtube
Derivative Of sin^2x, sin^2(2x) – The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variable Common trigonometric functions include sin(x), cos(x) and tan(x) For example, the derivative of f(x) = sin(x) is represented as f ′(a) = cos(a) f ′(a) is the rate of changeThe equation of tangent at point (x 1 , y 1) with slope m is given by \(\rm (y y_1) = m (x x_1)\) \(\rm (y {\pi}) = 2 (x \dfrac{\pi}{2})\) y = 2x Hence, the equation of the tangent line to the curve y = 2x sin x at the point \(\left(\frac \pi 2, \pi\right)\) is 2x Download Question With Solution PDF ››We have to prove that (tan x)^2 (sin x)^2 = (tan x)^2 * (sin x)^2 Start from the left hand side (tan x)^2 (sin x)^2 use tan x = sin x / cos x




Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions
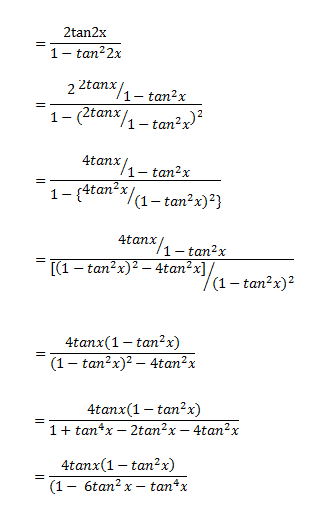



Trigonometry Functions Class Xi Exercise 3 3 Breath Math
FORMULAS TO KNOW Some trig identities sin2xcos2x = 1 tan2x1 = sec2x sin 2x = 2 sin x cos x cos 2x = 2 cos2x 1 tan x = sin x cos x sec x = 1 cos x cot x = cos x sin x csc x = 1 sin x Some integration formulas R xn dx = xn1 n1 C R 1 x dx = lnjxjC R ex dx = ex C R sin x dx = cos x C R cos x dx = sin xC R sec2 x dx = tan xC R tan x secOther calculators Integral Step by Step;Identities related to sin 2x, cos2x, tan 2x, sin3x, cos3x, and tan3x Sin 2x = Sin 2x = sin(2x)=2sin(x) cos(x) Sin(2x) = 2 * sin(x)cos(x) Proof To express Sine, the formula of "Angle Addition" can be used
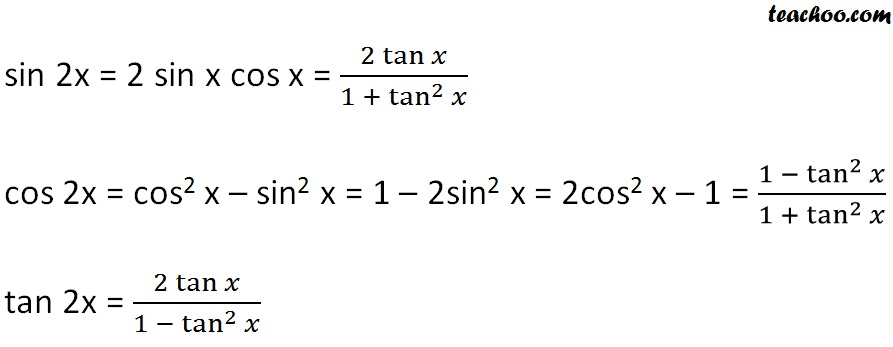



Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi



Q Tbn And9gcswqgrwxfu3ry9lhuwrnhzq Lnjumaniii4kgzg4 Wagpp Cjba Usqp Cau
Formulas from Trigonometry sin 2Acos A= 1 sin(A B) = sinAcosB cosAsinB cos(A B) = cosAcosB tansinAsinB tan(A B) = A tanB 1 tanAtanB sin2A= 2sinAcosA cos2A= cos2 A sin2 A tan2A= 2tanA 1 2tan A sin A 2 = q 1 cosA 2 cos A 2 = q 1cos A 2 tan 2 = sinA 1cosA sin2 A= 1 2 21 2 cos2A cos A= 1 2 1 2 cos2A sinAsinB= 2sin 1 2 (AB)cos 1 2 (A 1B These formulas can be derived using x y formulas For sin 2x sin 2x = sin (x x) Using sin (x y) = sin x cos y cos x sin y = sin x cos x sin x cos x = 2 sin x cos x For cos 2x cos 2x = cos (x x) Using cos (x y) = cos x cos y – sin x sin y = cos x cos x – sin x sin x = cos 2 x – sin 2 xNote that `tan^2x1=sec^2x=1/(cos^2x) ` and `tan^2x=(sin^2x)/(cos^2x) ` Substituting we get `(tan^2x)/(1tan^2x)=((sin^2x)/(cos^2x))/(1/(cos^2x))=sin^2x ` as required




Analytic Trig Ppt Video Online Download
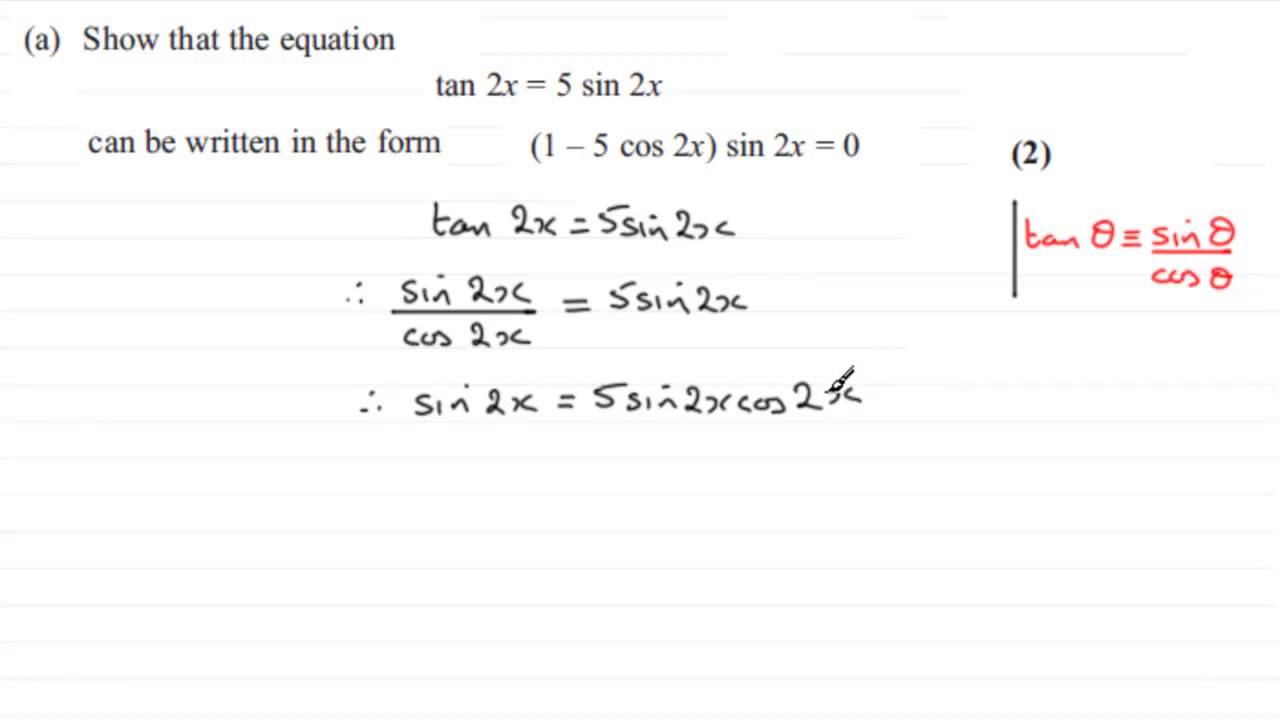



Edexcel Core Mathematics C2 June 12 Solutions Examples Worksheets Videos Activities
Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan(2x) = 2 tan(x) / (1The figure at the right shows a sector of a circle with radius 1 The sector is θ/(2 π) of the whole circle, so its area is θ/2We assume here that θ < π /2 = = = = The area of triangle OAD is AB/2, or sin(θ)/2The area of triangle OCD is CD/2, or tan(θ)/2 Since triangle OAD lies completely inside the sector, which in turn lies completely inside triangle OCD, we haveThere are easier equations to the halfangle identity for tangent equation tan x/2 = sin x/ (1 cos x) 1st easy equation tan x/2 = (1 cos x) /sin x 2nd easy equation Summary of HalfAngles • Sine o sin x/2 = ±√ (1 cos x)/ 2 • Cosine o cos x/2 = ±√ (1 cos x)/ 2 by Shavana Gonzalez



Www Mayfieldschools Org Downloads 4 8 double angle formulas answers Pdf




1 Sin 2 X Formula Sepertikisahku
Linear homogeneous differential equations of 2nd order StepByStep Another note The identity could be "rescued" as $$\sin(2x)\tan(2x)=2(\sin x)^2 \tan (2x)$$ With the common notation $\sin^2 x$ for the square of the sine, this means OP may have just been inexact on putting the exponent there, but it still needs that extra factor of $2$Trigonometry Solve for x cot (x)tan (x)=2/ (sin (2x)) cot(x) tan(x) = 2 sin(2x) cot ( x) tan ( x) = 2 sin ( 2 x) Simplify each term Tap for more steps Rewrite cot ( x) cot ( x) in terms of sines and cosines cos ( x) sin ( x) tan ( x) = 2 sin ( 2 x) cos ( x) sin ( x) tan ( x) = 2 sin ( 2 x) Rewrite tan ( x) tan ( x) in terms of sines and cosines




Calculate Sin2x Cos2x And Tan2x For Given Tanx In Quadrant 2 Youtube




Sin2x Cos2x 1 Proof
Inequalities Step by Step;Sin 2x = 2 sin x cos x Cos 2x = 2 cos2x − 1 Multiply the above two answers to get the value sin 2x cos 2x = (2 sin x cos x) (2 cos2x − 1) = 2 cos x (2 sin x cos2 x − sin x) Now, consider equation (i) and (iii), sin 2x = 2 sin x cos x cos 2x = 1 − 2 sin2xA Let cosx = () and cos x lies below the x axis Find sin(2x), cos(2x) and tan(2x) b Proof the formula of unit circle x?
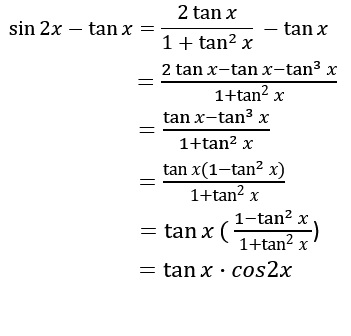



Sin2x Tanx Complete The Identity Socratic




Find Sin 2x Cos 2x And Tan 2x If Sinx 13 And X Chegg Com
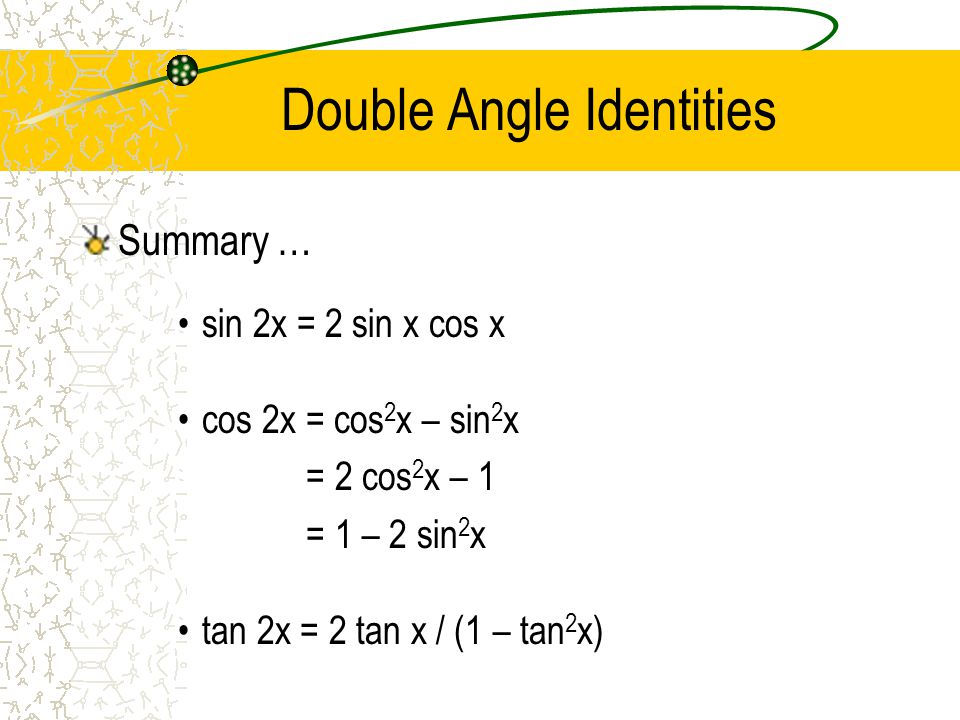
The double angle formulas can be derived by setting A = B in the sum formulas above For example, sin(2A) = sin(A)cos(A) cos(A)sin(A) = 2sin(A)cos(A) It is common to see two other forms expressing cos(2A) in terms of the sine and cosine of the single angle A Recall the square identity sin 2 (x) cos 2 (x) = 1 from Sections 14 and 23Tan(x)cot(x)=4sin(2x)tan(x)cot(x) = 8sin(x)*cos(x) Multiply thru by sin*cos sin^2 cos^2 = 8sin^2*cos^2 8sin^2cos^2 = 1 sin^2*(1 sinFree trigonometric equation calculator solve trigonometric equations stepbystep This website uses cookies to ensure you get the best experience By




Tan2x Sin2x Tan2x Sin2x 5 1 Brainly In



Cy6wx Xdh8picm
For each of the three trigonometric substitutions above we will verify that we can ignore the absolute value in each case when encountering a radical 🔗 For x = asinθ, x = a sin θ, the expression √a2 −x2 a 2 − x 2 becomes √a2−x2 = √a2−a2sin2θ= √a2(1−sin2θ)= a√cos2θ= acosθ = acosθ a 2 − x 2 = a 2 − a 2= 1, and explain it in your own wordsTan (x) is an odd function which is symmetric about its origin tan (2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin (2x) to cos (2x) sin (2x) = 2 sin (x) cos (x) cos (2x) = (cos (x))^2 – (sin (x))^2 = 1 – 2 (sin (x))^2 = 2 (cos (x))^2 – 1 Proof 71K views View upvotes ·




Tan2x ただの悪魔の画像



Ilectureonline
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsThe identities you need are$^{\dagger}$ $$ \sin(4x) = \color{red}{2} \sin(2x) \cos(2x)\\ \tan(2x) = \frac{\sin(2x)}{\cos(2x)} $$ Substitute both in $$ \tan(2x)\sin(4x) = 0$$ to get $$ (1 2 \cos^2(2x))\sin(2x) = 0 $$ which you should be able to factor into $3$ cases `cos 2x=12 sin^2x` `=12((12)/13)^2` `=12(144/169)` `=(1692)/169` `=(119)/169` Notice that we didn't find the value of x using calculator first, and then find the required value If we had done that, we would not have found the exact value, and we would have missed the pleasure of seeing the double angle formula in action )




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic



Find The General Solution For The Equation Sec 2 2x 1 Tan 2x Sarthaks Econnect Largest Online Education Community
Practice Example for Sin 2x If we want to solve the following equation Sin 2x = sinx, Π ≤ Π We will follow the following steps Step 1) Use the Double angle formula Sin 2x = 2 Sin x Cos x Step 2) Let's rearrange it and factorize 2Sinx Cosx – sinx = 0 Sin x (2 cos x 1) = 0Formula sin 2 θ = 2 tan θ 1 tan 2 θ A trigonometric identity that expresses the expansion of sine of double angle function in terms of tan function is called the sine of double angle identity in tangent functionThe trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is \(Sin 2x = 2 sin x cos x\) Where x is the angle Source enwikipediaorg Derivation of the Formula




Find Sin 2x Cos 2x And Tan 2x If Tan X 12 5 And X Terminates In Quadrant I Study Com




Ppt Multiple Angle Formulas Ts Making Decisions After Reflection And Review Powerpoint Presentation Id
List of Trigonometric sin2x cos2x tan2x tan3x theta formula/identity Proof in terms of tanx, sin3x cos3x formula/identity, sin2xcos2x sin square x plus cos square x, cos sin a cos sin b sin cos a plus minus sin cos b




What Is Integral Of Sin2x Tan2x Quora




Rd Sharma Solutions For Class 11 Chapter 11 Trigonometric Equations Updated For 21 22 Coolgyan Org



Sin 2x Cos 2x And Tan 2x




Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Download




Find Sin 2x Cos 2x And Tan 2x If Tan X 3 And X Gauthmath
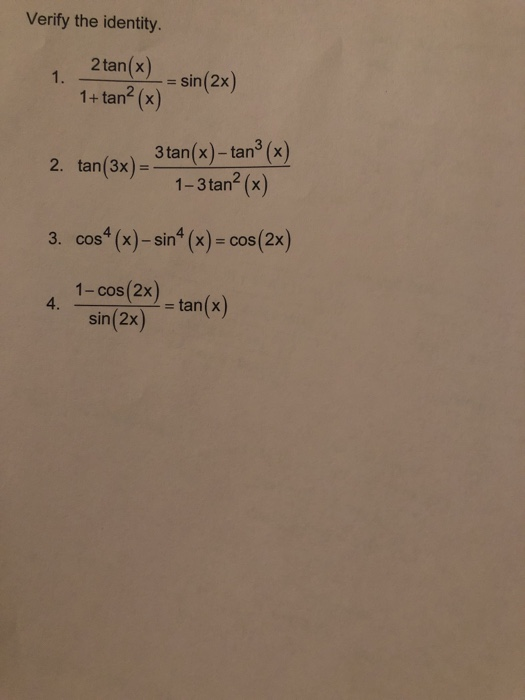



Verify The Identity 2tan X Sin 2x 1 Tan2 X 2 Chegg Com




5 5 Multiple Angle And Product Sum Formulas Find All Solutions In Ppt Download




Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube




Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Integrate Tan 2x By Parts



What Is The Formula Of Tan2x Quora




Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi




Math34 Trigonometric Formulas




Section 7 3 Double Angle Half Angle And Sum



Section 2 Identities Cofunction Double Angle Half Angle Ppt Video Online Download
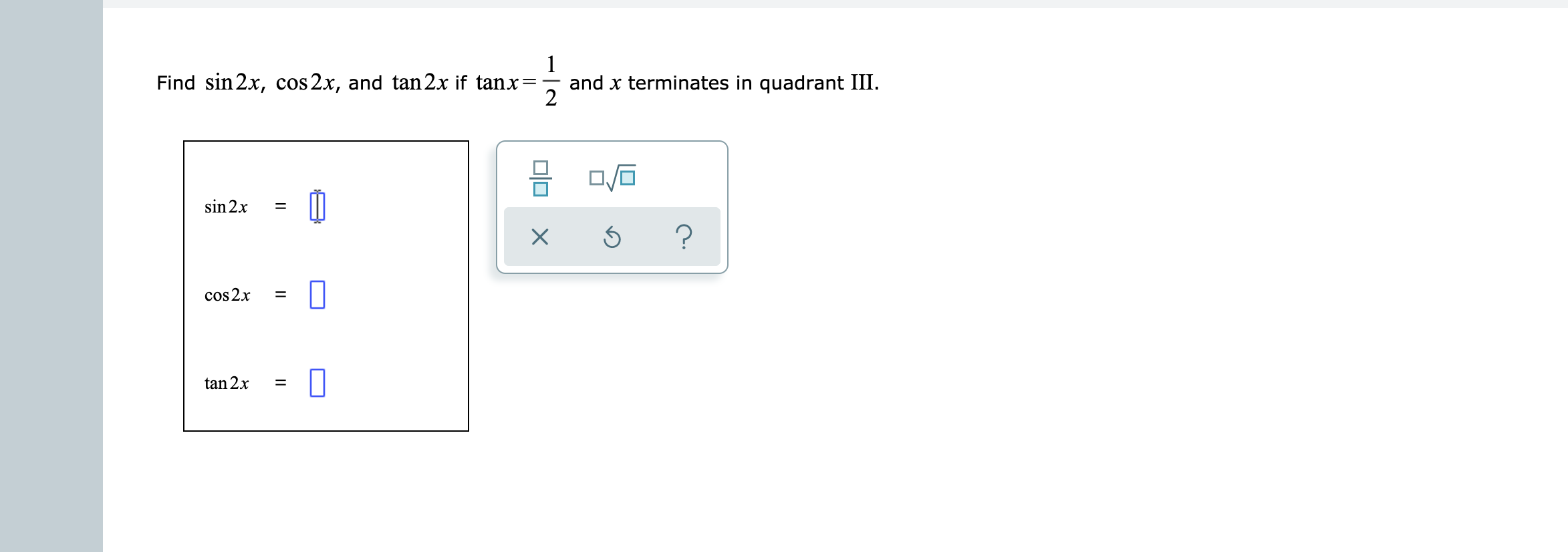



Answered 1 Find Sin 2x Cos 2x And Tan 2x If Bartleby



How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora




Tangent Half Angle Formula Wikipedia




Tan 2 X Tan 2 X 1 Cosec 2 X Sec 2 X Cosec 2 X 1 Sin 2 X Cos 2 X Brainly In




Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Lesson 4 5 Double Angle Formulas
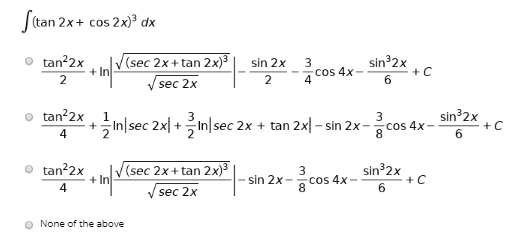



Answered Stan 2x Cos 2x Dx Tan 2x 2 V Sec 2x Bartleby



Sin 2x Formula Sin 2theta Formula Practice Examples
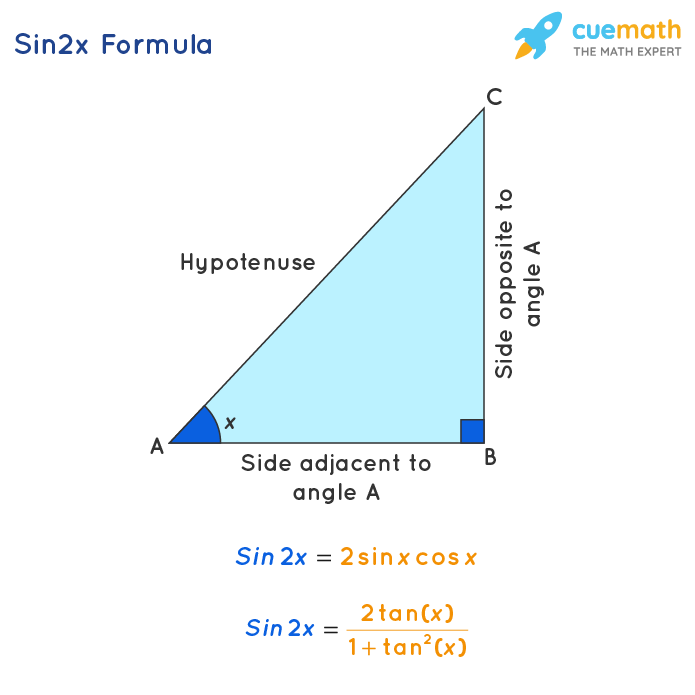



Sin 2x Formula What Is Sin 2x Formula Examples




If Sin X 1 5 And X Is In Quadrant I Find The Exact Values Of The Expressions Without Solving For X Wyzant Ask An Expert




Using Double Angle Formulas Objective To Apply The Double Angle




If Tan X 2tan 2x 3tan 3x 8cot 8x 3 Then The General Solution Of X




Cos2x 1 Sin2x Tan Pi 4 X Double And Half Angle Identity Youtube



Sites Math Washington Edu Putnam Handouttrig Pdf




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube




Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help




Double Angle Identities Solutions Examples Videos Worksheets Games Activities




Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Answered 3 10 Double Angle Formulas Find Sin Bartleby




Section 7 3 Double Angle Half Angle And Sum
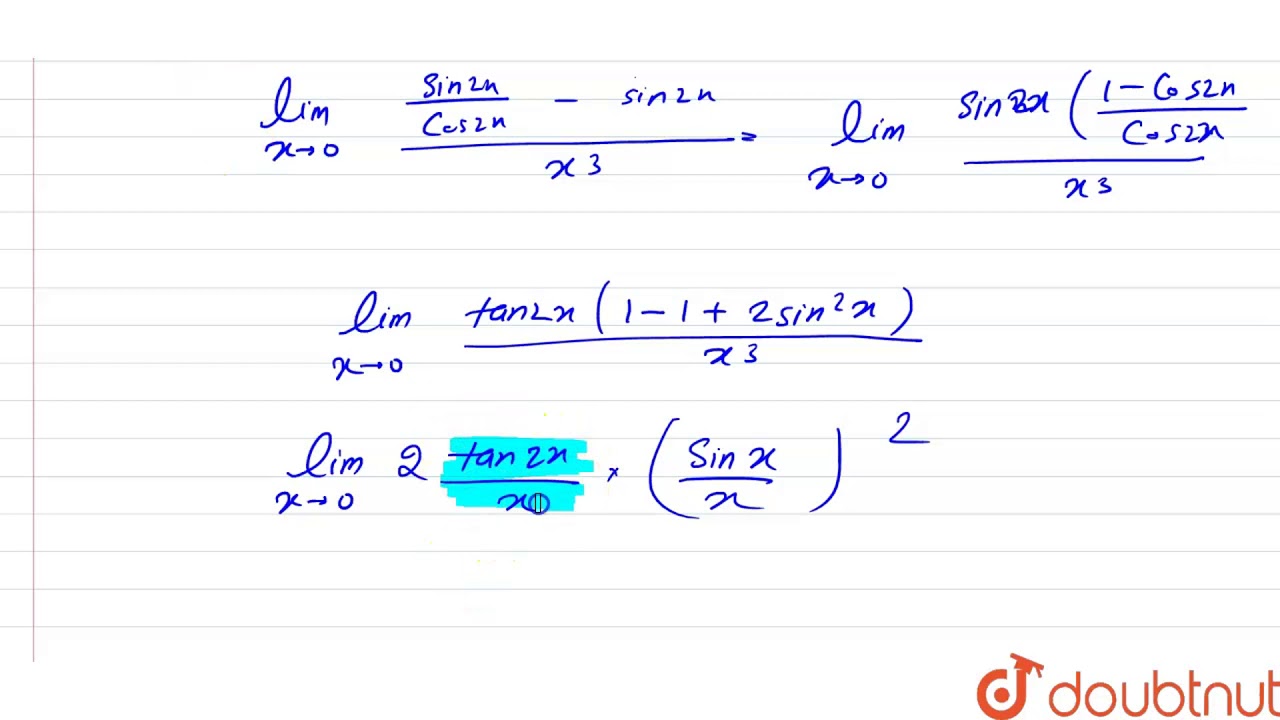



Evaluate The Following Limits Lim Xto0 Tan2x Sin2x X 3 Youtube
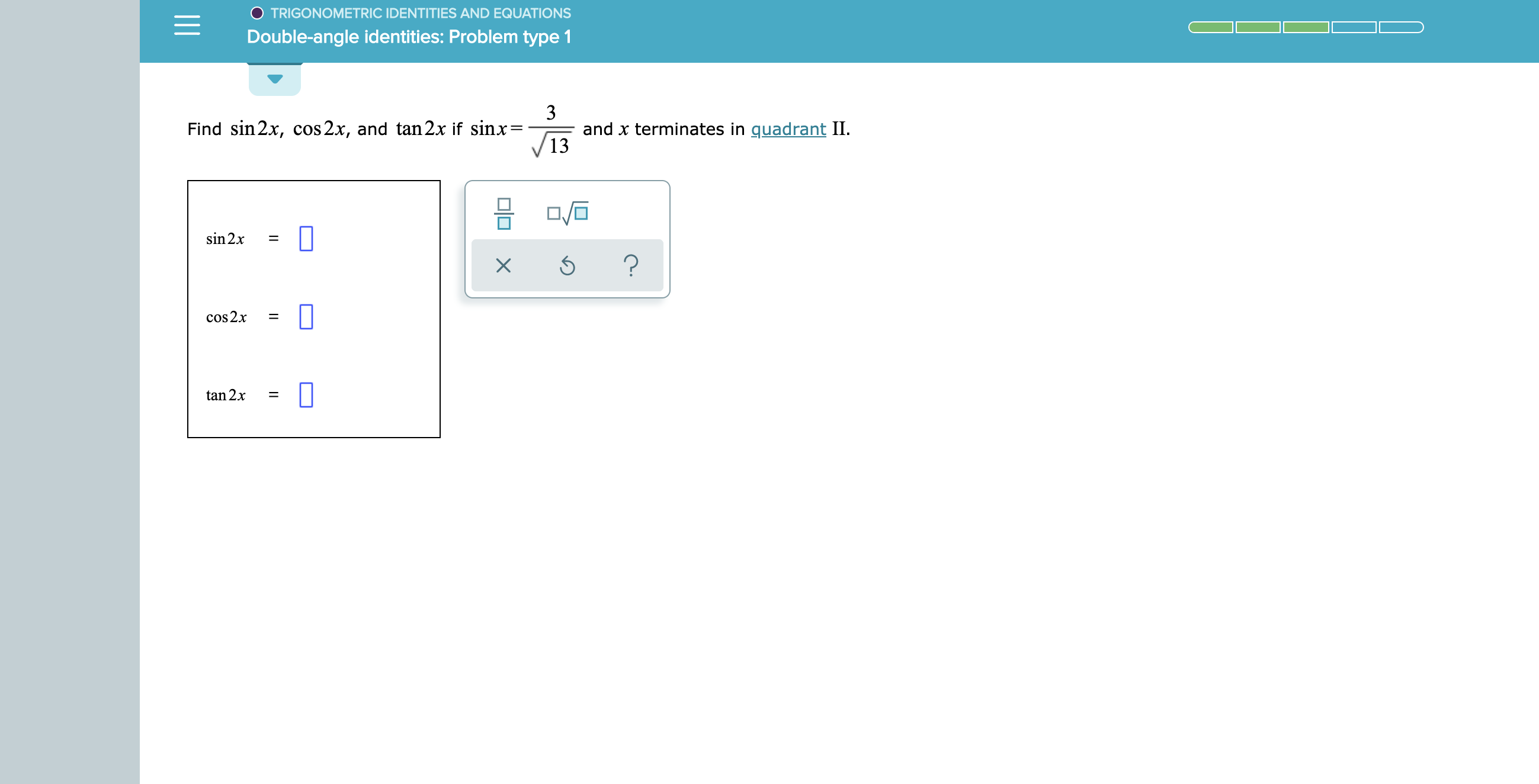



Answered Trigonometric Identities And Equations Bartleby




Solved 3 10 Double Angle Formulas Find Sin 2 X




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic
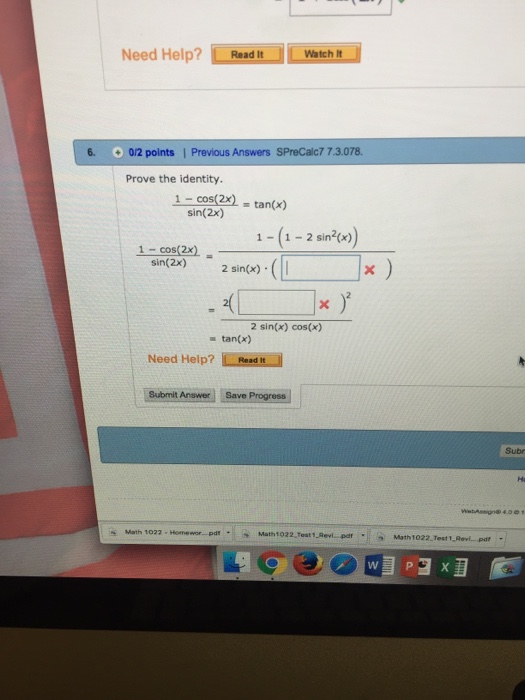



Prove The Identity 1 Cos 2x Sin 2x Tan X 1 Chegg Com




Double Angle Properties Rules Formula Examples Video Lesson Transcript Study Com
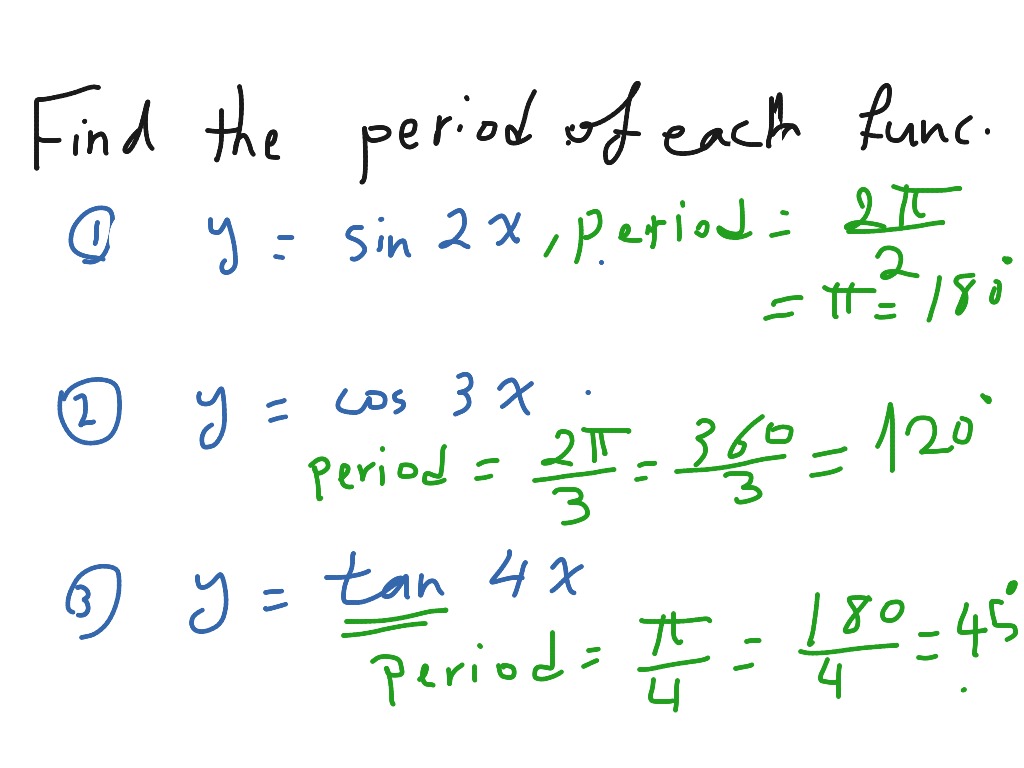



Find The Period Of Sin2x Cos 3x Tan 4 X Math Trigonometry Showme
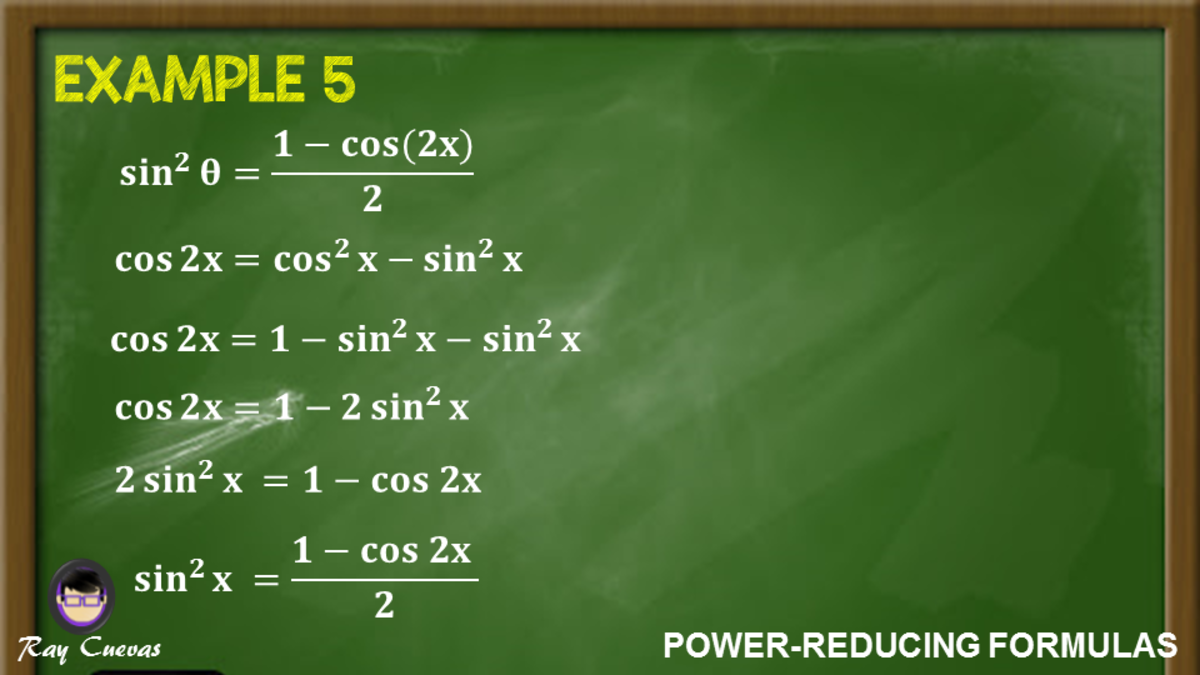



Power Reducing Formulas And How To Use Them With Examples Owlcation




Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube



What Are The Formulas Of Sin 2x Quora
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




Verify The Identity 2 Tan X Sin 2x 1 Tan2 X 2 Chegg Com




Tan2x ただの悪魔の画像



3




Tangent Half Angle Formula Wikipedia



Http Www Mayfieldschools Org Downloads 4 8 double angle formulas key Pdf




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




Tan 2x Sin 2x Tan 2xsin 2x Wyzant Ask An Expert




Find Sin 2x Cos 2x And Tan 2x If If Tan X 2 And Gauthmath




Section 7 3 Double Angle And Half Angle Formulas Flashcards Quizlet



Prove Sin2x 2tanx 1 Tan 2x Socratic




Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2



Prove The Identity Cos 2x 1 Sin 2x Tan P 4 X Sarthaks Econnect Largest Online Education Community
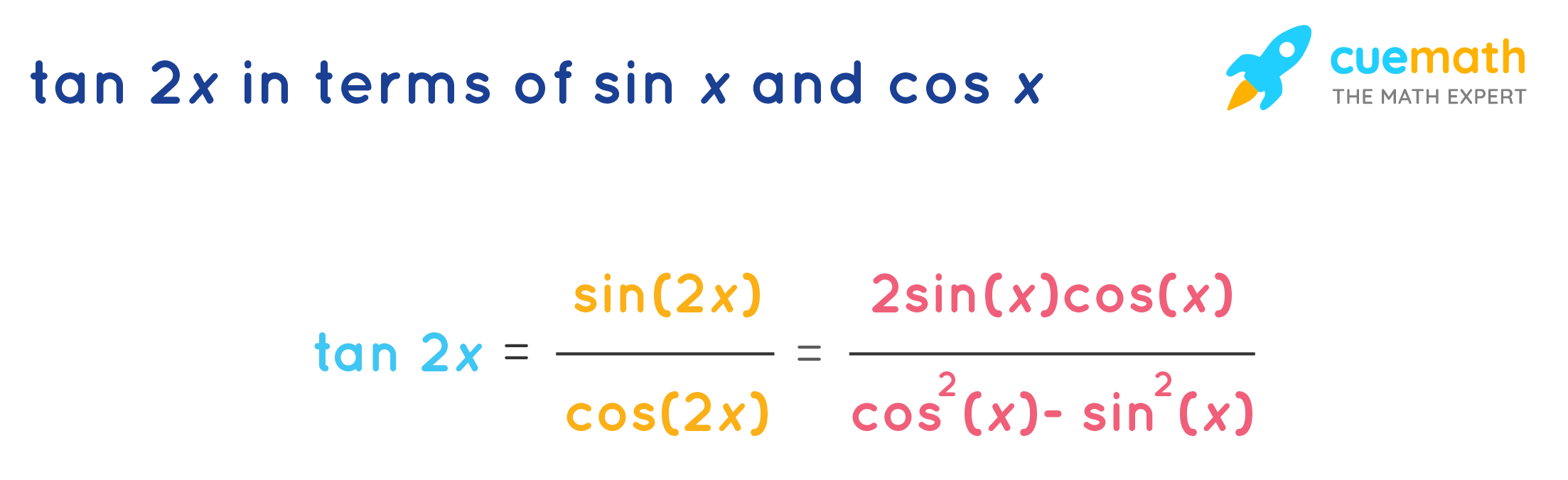



Tan 2x Formula What Is Tan 2x Formula Examples




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube




Int Dx Sin 2x Tan 2x



What Is The Formula Of Tan2x Quora



Tan2x ただの悪魔の画像




Trig Double Identities Trigonometric Double Angle Functions Trig




Sin 2 X Dawonaldson




Tan 2x Sin 2x Tan 2xsin 2x Brainly In




Sin 2x Formula Trigonometry Formula




Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com



1
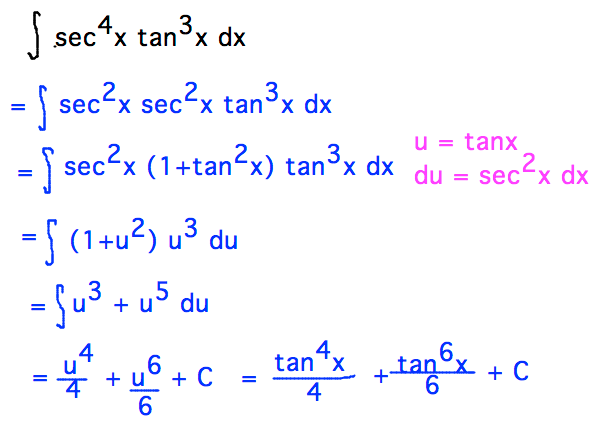



Geneseo Math 222 01 Trigonometric Integration




Tan 2x Sin 2x Tan 2x Sin 2x
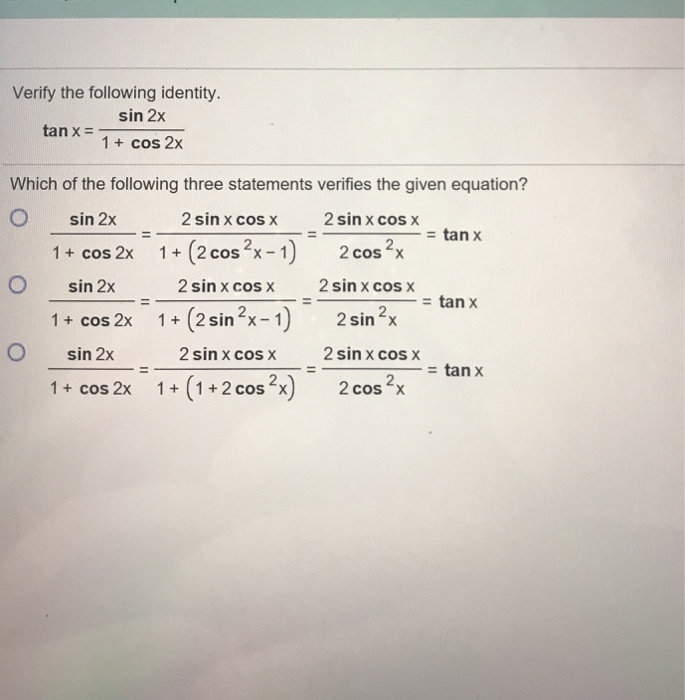



Verify The Following Identity Tan X Sin2x 1 Cos Chegg Com




Trigonometric Identity In Double Angle Sin2x Cos2x 1 Sin2x Cos2x 1 Sec2x Tan2x Youtube



What Is The Formula Of Tan2x Quora
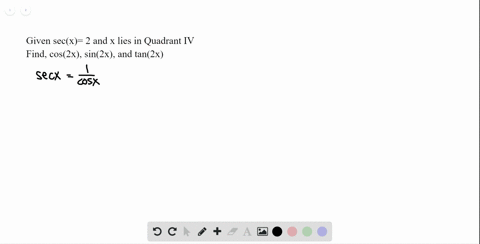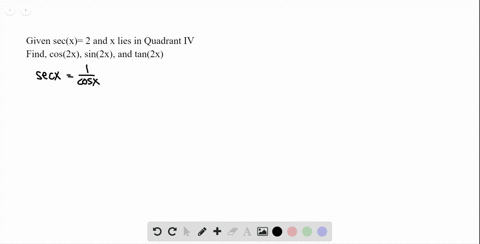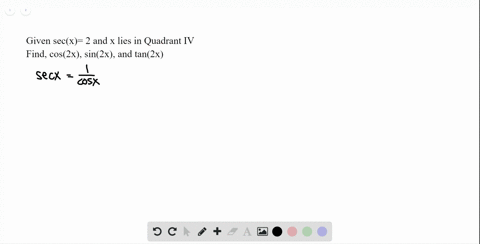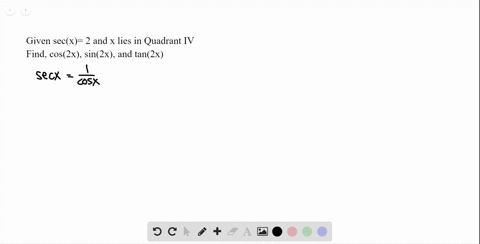



Solved 3 10 Double Angle Formulas Find Sin 2 X




Tan 2x Formula What Is Tan 2x Formula Examples


